Es un error bastante frecuente que el estudiante novato confunda la energía con la potencia en el diseño de sistemas eléctricos. Esto ocurre todavía con más asiduidad cuando se trata de una instalación solar o en la compra de un kit fotovoltaico. Por ello, es muy importante, antes de hacer cualquier inversión en esta tecnología, tener claro que la potencia se define a partir de la energía.
La energía eléctrica es aquella forma de energía que es capaz de generar una diferencia potencial en un espacio determinado de manera que se cree una corriente eléctrica, esto es carga cargas eléctricas, como los electrones, en movimiento. Como es de sobra sabido, el movimiento de estas cargas eléctricas puede ser aprovechado para generar trabajo en multitud de aplicaciones, como por ejemplo, la iluminación, la electrónica, los motores eléctricos, etc. En resumen, lo que ocurre cuando se utiliza energía eléctrica para una de estas aplicaciones es que la misma se transforma en otro tipo de energía: lumínica, cinética, calorífica, etc. En ese sentido, la energía eléctrica se consume.
La unidad del sistema internacional (SI) para medir cualquier tipo de energía es el Julio (J). No obstante, es común expresar algunos tipos de energía en otras unidades; así por ejemplo, la energía que contienen los alimentes suele expresarse en kilocalorías (kCal), que por supuesto tiene su equivalente en Julios, en concreto: 1 kCal = 4184 J.
Por su lado, la potencia eléctrica es la capacidad que tiene un dispositivo de consumir o generar energía eléctrica durante un tiempo determinado. La unidad de sistema internacional para la potencia es el vatio (W), que se define a partir de la siguiente expresión:
E = P ✕ t → P = E/t
donde E simboliza la energía, P la potencia y t el tiempo. Si expresamos la energía y el tiempo en sus unidades SI (es decir, en Julios y segundos), se obtiene:
P = E/t → 1 W = 1 J/s → [W] = [J/s]
Por lo tanto, un vatio es el cociente entre un Julio y un segundo. Como el Julio es una unidad muy pequeña comparada con los grandes consumos eléctricos que se dan convencionalmente en las aplicaciones eléctricas más comunes, se convino que la energía eléctrica tuviera como base el consumo de un dispositivo de 1000 W de potencia durante una hora, es decir:
E = P ✕ t → E = 1000 W ✕ 1 h → E = 1 kW ✕ 1 h = 1 kWh.
Por lo tanto, el consumo eléctrico se indica normalmente en kilovatios-hora (kWh) o en vatios-hora (Wh), pero nunca en vatios (W), ya que, como se ha visto, los vatios es una unidad de potencia no de energía. Así, un dispositivo eléctrico se caracteriza por su potencia, cuanta más potencia más consumo tendrá el dispositivo por unidad de tiempo. Por todo lo anterior, la equivalencia Julio-kWh es:
1 kWh = 1000 Wh = 1000 W✕ 3600 s = 3.6 ⋅106 J → 1 J = 2.77 ⋅10-7 kWh.
Todo lo anterior sirve tanto para sistemas que consumen como para aquellos que generan energía eléctrica, como son los módulos fotovoltaicos. En ese sentido, un módulo fotovoltaico viene caracterizado por la potencia máxima a la que puede trabajar, es decir, cuando existen unas condiciones concretas llamadas standard test conditions (STC), caracterizadas por una irradiancia de I = 1 kW/m², una temperatura del módulo de 25 ºC y una masa de aire de 1.5. Por ejemplo, el módulo de la primera figura será capaz de generar 200 W de energía eléctrica, si se expone al Sol y se dan unas condiciones STC. Si estas condiciones se mantienen, por ejemplo, durante 3 horas, entonces el módulo generará una energía de:
E = P ✕ t = 200 W ✕ 3 h = 600 Wh = 0.6 kWh.
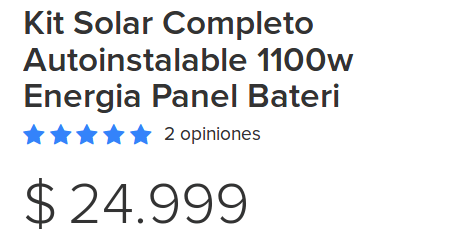
Con todo, existen muchos vendedores de kits fotovoltaicos que confunden la energía con la potencia. Por ejemplo, en una conocida página web de compra y venta, encontramos el siguiente anuncio.
Como se observa, se vende un kit fotovoltaico de 1100 W por 25000 $AR, lo que es un precio excelente, ya que sale a unos 22 $AR/W. Siempre que entendamos que esos 1.1 kW se refiere a la suma de la potencia máxima de los módulos fotovoltaicos incluidos en el kit. No obstante, fijándonos en las especificaciones de la oferta, vemos lo siguiente:
Es decir, el kit solo lleva un solo módulo de 150 W, por lo que esa es la potencia real. Además lleva, un inversor de 1000 W, pero los inversores no generan energía, sino que simplemente convierten la corriente continua (CC) de las baterías en corriente alterna (CA). Es decir, con las baterías llenas el inversor puede puntualmente entregar una potencia máxima de 1000 W. Así pues, no queda claro a que se refiere el vendedor con esos “1100 W por día”, ya que al ser los vatios una unidad de potencia no tiene sentido evaluarla de esa forma.
Para estimar cuanta energía puede generar este kit al día es necesario saber la irradiación media del lugar donde vaya a instalarse. Por ejemplo, en la provincia de Buenos Aires, la irradiación media en verano es de 6.6 kWh/m², por lo que en esa época el kit podrá suministrar una energía máxima de 0.150 ✕ 6.6 = 1 kWh/día, mientras que durante el invierno, la radiación es de 2 kWh/m², por lo que la electricidad máxima producida podría ser: 0.150 ✕ 2 = 0.3 kWh/día.
A la luz de estos datos se puede suponer que lo que quería expresar el fabricante era que el sistema es capaz de generar 1100 Wh/día, o lo que es lo mismo, 1.1 kWh/día, pero se le olvidó añadir las horas “h” a las unidades. Este es un error bastante común. No obstante, ahora sabemos que esa energía solo la generará en los mejores días del verano, por el contrario en invierno la producción será mucho menor. En conclusión, a la hora de adquirir un kit solar es fundamental preguntar por la potencia máxima de los módulos fotovoltaicos que lo componen y realizar unos pequeños cálculos estimativos con la irradiación solar media del lugar para hacerse una idea de la energía que se espera produzca el sistema.







Deja tu comentario
Debe iniciar sesión para escribir un comentario.